Współczynniki Greckie

Współczynniki greckie

Na wartość opcji wpływa 5 czynników:

• Ceny instrumentu bazowego
• Ceny wykonania
• Wolnej od ryzyka stopy procentowej
• Zmienności instrumentu pierwotnego
• Czasu do wygaśnięcia opcji

Aby ułatwić ich wycenę wymyślono współczynniki greckie, które pozwalają określić zmianę wartości opcji wskutek zmiany powyższych elementów. Oprócz swej podstawowej roli współczynniki greckie pozwalają również zarządzać ryzykiem, zabezpieczając portfel przed zmianami tych czynników. Współczynniki greckie, poprzez badanie wrażliwości premii, umożliwiają bardziej szczegółową analizę pojedynczego kontraktu opcyjnego, jak również strategii złożonych.

Platforma xOption na bieżąco liczy aktualne wielkość współczynników.

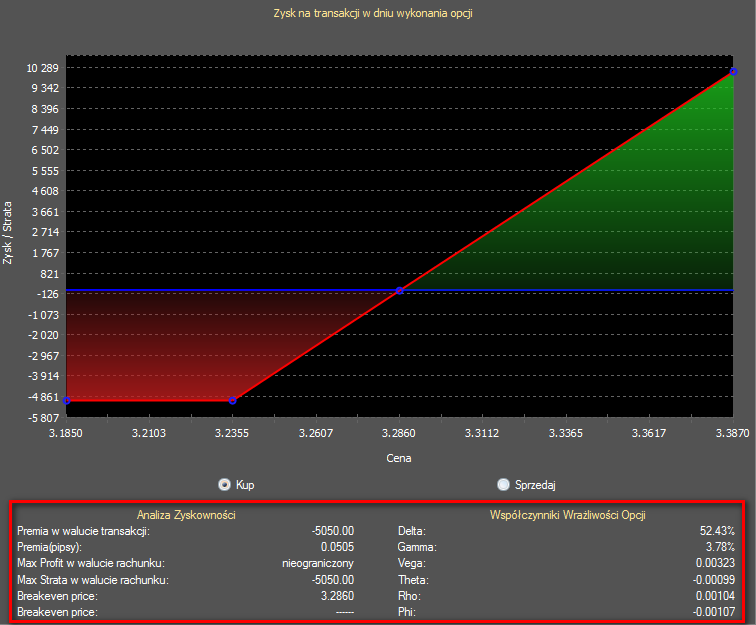
Delta

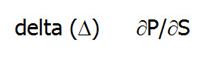
Delta jest prawdopodobnie najpopularniejszym współczynnikiem greckim, a pokazuje jak duże jest teoretyczne prawdopodobieństwo zrealizowania opcji z zyskiem. Określa o ile zmieni się wycena opcji (premia opcyjna), jeżeli wartość instrumentu bazowego zmieni się o 1 punkt (krańcowy przyrost ceny opcji względem krańcowego przyrostu kursu spot). Delta liczona jest z pierwszej pochodnej ceny opcji i jest wyrażona w procentach. Jeżeli wartość delty naszej opcji wynosi 60%, a kurs danego instrumentu bazowego zmieni się o 60 pipsów, to cena (premia) danej opcji zmieni się o: 60% x 60 pipsów = 36 pipsów. W skrócie można przyjąć, że delta na poziomie 60% daje 60% szansę osiągnięcia zysku z zakupionej opcji. Dla sprzedającego opcję szansa ta wynosi 40%.

Z punktu widzenia wysokości premii oraz ceny wykonania instrumentu bazowego, opcje możemy podzielić na trzy kategorie:

• OTM (out the money, „poza pieniądzem”) – niska premia
• ATM (at the money, „na pieniądzu”) – umiarkowana premia I
• TM (in the money, „w pieniądzu) – wysoka premia. Przedziały Delty dla poszczególnych rodzajów opcji:

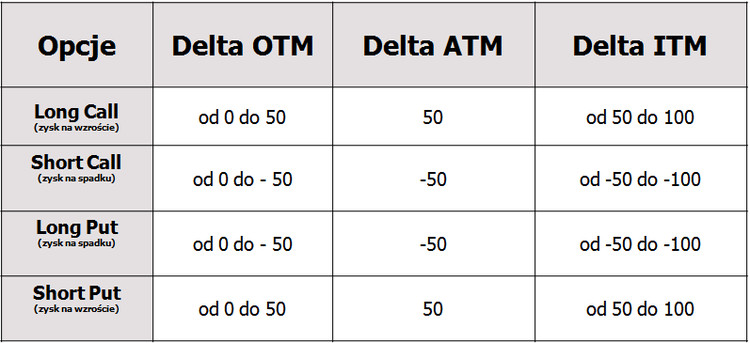
Jak widać, Delta dla opcji zyskujących na wzrostach ma znak dodatni, a dla opcji zyskujących na spadkach – ujemny.

Gamma

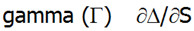
Kolejnym współczynnikiem jest Gamma. Gammę liczy się z drugiej pochodnej ceny opcji w stosunku do kursu instrumentu bazowego i mówi o ile zmieni się wielkość Delty, jeżeli wartość instrumentu bazowego zmieni się o 1 punkt. Najbardziej opłacalne dla kupującego są opcje o wysokiej gammie, bowiem wysoka Gamma powoduje znaczne zmiany Delty. Najwyższą wartość Gammy posiadają z kolei opcje ATM (at-the-money) oraz blisko terminu wygaśnięcia. Należy pamiętać, iż Gamma jest dodatnia dla opcji kupionych, a ujemna dla opcji wystawionych. Reasumując. Kupujący opcję z ujemną Gammą liczy na stabilizację ceny instrumentu bazowego i trend horyzontalny. Z kolei kupujący opcję z dodatnią Gammą oczekują dużej zmienności kursu bez znaczenia w jakimkolwiek kierunku to nastąpi.

Przykład

Jeżeli założymy wartość Delty na poziomie 60%, a Gammy 0,0200 to zmiana kursu instrumentu bazowego o 1 punkt spowoduje wzrost Delty do poziomu 61%.

Theta

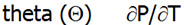
Współczynnik theta jest pochodną ceny opcji względem i mierzy o ile spadnie cena/premia opcji w skutek upływu danej jednostki czasu (standardowo, jak i na platformie xOption jednostką czasu jest 1 dzień). Theta ma zatem związek z wartością czasową opcji. Upływ czasu skutkuje spadkiem wyceny opcji. Upływ czasu jest korzystny na wystawcy opcji i negatywny dla kupującego. Z tego też względu Theta dla opcji kupionych (long) jest ujemna, a dla opcji sprzedanych dodatnia. Najwyższą Thetę posiadają opcje ATM (at-the-money) oraz opcje krótkoterminowe. Krótki okres do wygaśnięcia opcji, sprawia, że każdy upływający dzień jest więcej wart, zarówno dla kupującego (mocny spadek wyceny opcji) jak i sprzedającego (mocny wzrost wyceny). Wraz z upływającym czasem, opcje In oraz Out Of The Money zmniejszają, a opcje At The Money zwiększają wartość Theta. Przykład 1 Jeżeli premia opcyjna wynosi 100, a Theta wynosi +1 to po upływie 1 dnia (przy niezmienionych innych czynnikach) premia wzrośnie do 101.

Przykład 2

Ile wyniesie nowa wartość opcji jeśli w wyniku upływu 10 dni? Wartość opcji = 0,40 Czas do wygaśnięcia = 80 dni Theta opcji = 0,0015 Obliczenia: Wartość opcji spadnie o 0,015 = 0,0015 x 10 Nowa wartość opcji 0,385 = 0,40 – 0,015

Vega

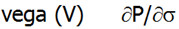
Współczynnik Vega jest pierwszą pochodną premii opcyjnej i mierzy, o ile zmieni się wartość premii opcyjnej, jeżeli zmienność (volatility) instrumentu bazowego zmieni się o 1 punkt procentowy (1%). Jest to zatem wskaźnik opisujący wrażliwość premii na zmianę wahań ceny waloru. Vega przyjmuje wartości dodatnie dla opcji kupionych, co oznacza, że wzrost zmienności zwiększa wartość kupionej opcji. Z kolei wartości ujemne charakterystyczne są dla sprzedających opcje, a więc wzrost zmienności powoduje spadek ceny opcji. Najbardziej czułe na zmienność instrumentu bazowego są opcje ATM (at-the-money) i to właśnie one przyjmują najwyższą wartość tego parametru. Innymi słowy, kupujący opcję z dodatnią Vegą oczekuje wzrostu zmienności implikowanej (rynkowej), co można łączyć z oczekiwaniem dużych zmian kursu spot w dłuższej perspektywie. Natomiast inwestor liczący na spadek zmienności instrumentu powinien szukać opcji z Vegą ujemną. Vega rośnie wraz długością trwania opcji (matematycznie: wariancja jest liniowa względem czasu), dlatego też długi okres do wygaśnięcia opcji zwiększa niepewność co do jej rozliczenia z zyskiem i zwiększa prawdopodobieństwo wystąpienia dużej zmienności, a to powoduje wyższą wartość Vegi.

Przykład 1

Jeżeli premia opcji wynosi 100 punktów, a Vega wynosi 3, to wzrost zmienności o 1% spowoduje wzrost premii do 103 punktów. Przykład 2 Ile wyniesie nowa wartość opcji w wyniku spadku zmienności instrumentu bazowego o 2%? Wartość opcji = 1,68 Zmienność instrumentu bazowego = 10% Czas do wygaśnięcia = 80 dni Kappa (Vega) opcji = 0,22 Obliczenia: Wartość opcji spadnie o 0,44 = 0,22 x 2 Nowa wartość opcji 1,24 = 1,68 – 0,44 RHO

Współczynnik Rho

Wspołczynnik Rho mierzy, o ile zmieni się premia opcyjna (wycena opcji), jeżeli oprocentowanie waluty kwotowanej (druga waluta w parze) lub stopy wolnej od ryzyka zmieni się o 1 punkt procentowy. Liczy zmianę wartości opcji na wskutek zmiany wolnej od ryzyka stopy procentowej. Jeżeli inwestor prognozuje wzrost stóp procentowych waluty kwotowanej powinien skupić się na opcjach posiadających Rho dodatnie. Natomiast inwestor prognozujący obniżkę stóp procentowych waluty kwotowanej powinien skupić się na opcjach posiadających Rho ujemne.

Strategia Znak rho

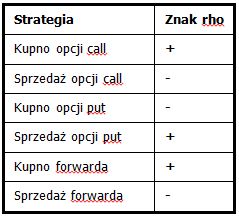
Kupione opcje in-the-money mają największą, a opcje out-of-the-money najmniejszą wartość Rho. Z kolei sprzedane opcje in-the-money mają największą ujemną, a opcje out-of-the-money najmniejszą ujemną wartość Rho. Przykład 1 Ile wyniesie cena opcji, jeżeli wolna od ryzyka stopa procentowa wzrośnie o 0,5%? Wartość opcji Kupna = 4,35 Sprzedaży = 4,11 Wartość rho dla opcji Kupna = +0,0551 Sprzedaży = – 0,0561 Wolna od ryzyka stopa = 5% Obliczenia: Opcja kupna wzrośnie o 0,02755 = 0,5 x 0,0551 Opcja sprzedaży spadnie o 0,02805 = 0,5 x 0,0561 Nowa cena opcji wyniesie: Opcja kupna 4,378 = 4,35 + 0,0276 Opcja sprzedaży 4,082 = 4,11 – 0,028 PHI

Współczynnik Phi wskazuje, o ile zmieni się premia opcyjna (wycena opcji), jeżeli oprocentowanie waluty bazowej zmieni się o 1 punkt procentowy (dodatnia dla opcji zyskujących na spadkach).

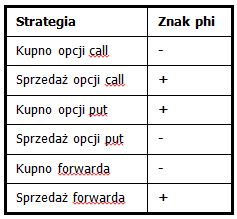
Gdy pozycja ma Phi dodatnie – inwestor oczekuje wzrostu stóp procentowych waluty bazowej. Natomiast gdy pozycja ma Phi ujemne – inwestor oczekuje obniżki stóp procentowych waluty bazowej.